1. 배열 (Array)
같은 type의 연관된 데이터를 효율적으로 관리하기 위한 자료구조.
장점 : index를 통해 원하는 위치에 있는 값에 대해 효율적으로 접근 할 수 있음.
단점 : 크기가 정해져 있으므로 유동적인 데이터의 추가, 삭제가 어려움.
시간 복잡도 :
접근 - O(1) [Index를 통해 값에 바로 접근]
검색 - O(n) [처음 Index부터 순회]
추가, 삭제 - 맨 뒤에 추가, 삭제 시 O(1), 중간 값일 시 추가, 삭제 후 데이터를 한칸씩 밀어야 하므로 O(n)
코틀린에서의 Array는 다음과 같이 사용할 수 있다.
// 크기 3의 배열 [1, 2, 3]
val array: Array<Int> = arrayOf(1, 2, 3)
// 크기 5의 배열 [0, 0, 0, 0, 0]
val array2: Array<Int> = Array(5) { 0 }
// 크기가 고정되어 있으므로 추가 시에는 left value를 통해 새로운 배열을 만들어야 함
val newArray = array.plus(3)
위와 같이 크기가 고정되어 있는 단점이 존재하므로, 코틀린에서는 ArrayList와 같은 크기가 자유롭고 추가, 수정 ,삭제가 용이한 타입을 제공한다.
// ArrayList [1, 2, 3]
val arrayList: ArrayList<Int> = arrayListOf(1, 2, 3)
// 기존 arrayList에 4이라는 값 추가 [1, 2, 3, 4]
arrayList.add(4)
// 기존 arrayList에 index 0의 값 삭제 [2, 3, 4]
arrayList.removeAt(0)
// 기존 arrayList에 2라는 값 삭제 [3, 4]
arrayList.remove(2)
2. 스택 (Stack)
목록의 끝에서만 접근 할 수 있는 제한적인 자료구조.
LIFO (Last In First Out) : 마지막에 들어온 데이터가 가장 먼저 나감
시간 복잡도 :
접근, 검색 - O(n) [처음 Index부터 순회]
추가, 삭제 - O(1) [마지막 index에 대해서 추가, 삭제 보장]

활용 :
웹 브라우저 뒤로가기(가장 나중에 열린 페이지를 먼저 보여줌)
역순 문자열 출력 (문자열의 마지막부터 출력) 등
코틀린에서도 Stack type을 지원한다.
val stack = Stack<Int>()
// 값 추가 (push)
stack.push(3)
stack.push(4)
// 값 추출 (pop), LIFO 구조를 가지므로 가장 마지막에 들어온 4가 pop 된다.
println(stack.pop()) // 4
3. 큐 (Queue)
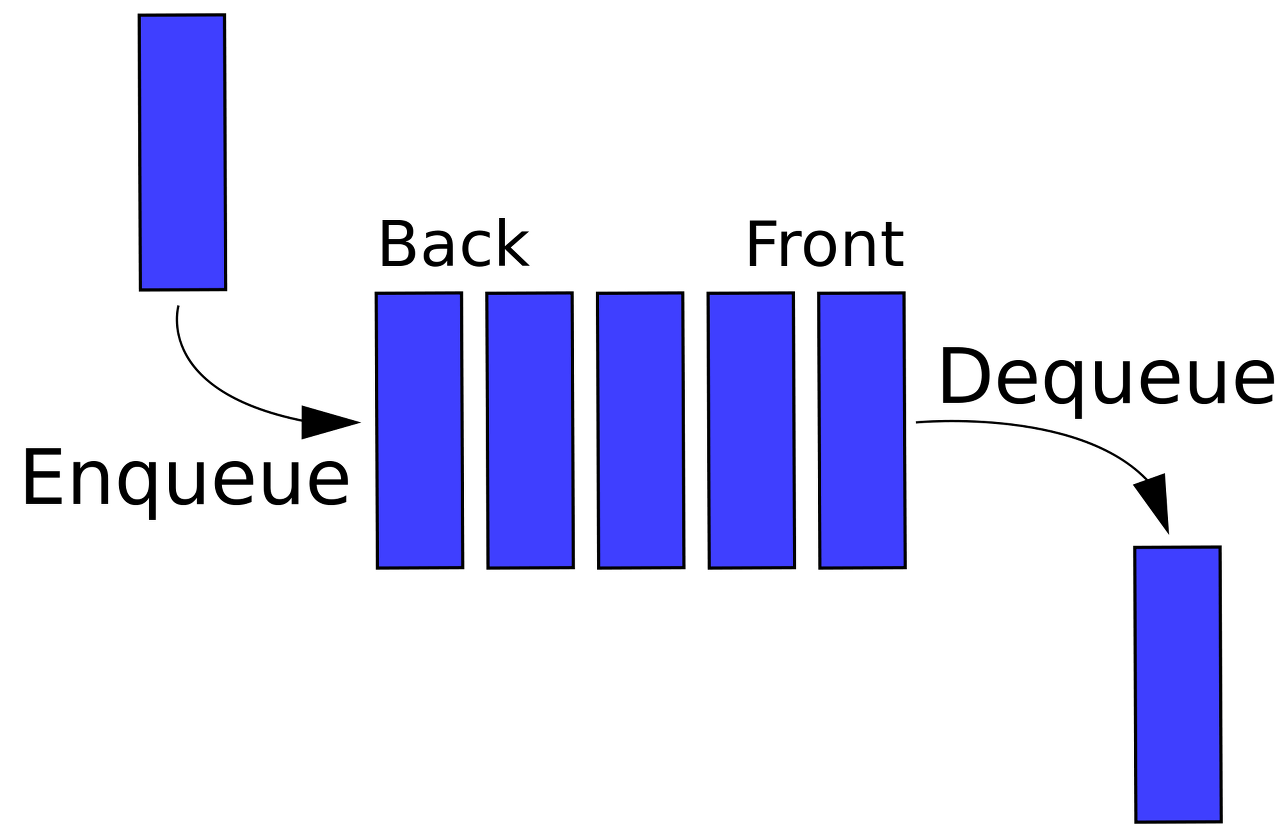
LIFO 형태를 가지는 스택과 반대되는 개념. 한쪽 끝에서는 삽입, 한쪽 끝에서는 추출 작업이 이루어짐.
FIFO (First In First Out) : 처음에 들어온 데이터가 가장 먼저 나감
시간 복잡도 :
접근, 검색 - O(n) [처음 Index부터 순회]
추가, 삭제 - O(1) [ 마지막 index에 추가, 처음 index 대해서 삭제 보장]
활용 :
프로세스의 스케줄링 (먼저 들어온 작업에 대한 처리)
BFS (너비 우선 탐색) 등
코틀린에서도 역시나 Queue type을 사용할 수 있다.
그러나 Queue는 클래스가 아닌 인터페이스이며, 이를 구현하는 다양한 클래스가 존재한다.(AbstractQueue, LinkedList ..)
그러므로, Queue type을 사용하기 위해서는 이를 구현하는 클래스의 인스턴스를 선언하여 사용한다.
val queue: Queue<Int> = LinkedList()
// 값 추가 (add or offer)
// add의 경우 에러 발생 시 Throw Exception을 수행함
queue.add(3)
queue.offer(4)
// 값 추출 (remove or poll), FIFO 구조를 가지므로 가장 먼저 들어온 3이 dequeue 된다.
// remove의 경우 에러 발생 시 Throw Exception을 수행함
println(queue.remove()) // 3
println(queue.poll()) // 44. 링크드리스트 (Linked List)
data, pointer를 가지는 각 노드가 연결되어 있는 형태의 자료구조.
노드를 연속적으로 연결함으로써 배열과 달리 동적인 크기를 가질 수 있음.
장점 : 노드의 중간지점에서의 자료의 추가, 삭제가 O(1)의 시간 복잡도를 가짐.
단점 : 데이터를 검색하기 위해서는 head부터 순회해야 하므로 O(n)의 시간 복잡도를 가짐.
시간 복잡도 :
접근, 검색 - O(n) [처음 Index부터 순회]
추가, 삭제 - 맨 앞 또는 뒤라면 O(1), 중간 위치라면 O(n)
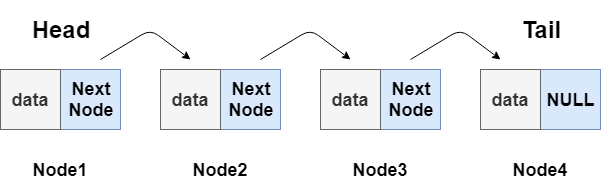
단일(Single) 링크드리스트 : 하나의 pointer를 가지며, next node만을 가리킴.
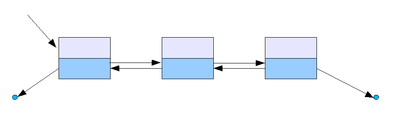
이중(Double) 링크드리스트 : 두개의 pointer를 가지며 이전(prev), 다음(next) node를 가리킴.
원형(Circular) 링크드리스트 : 일반적인 링크드리스트에서, 마지막 노드가 처음 노드를 가리킴.

코틀린에서도 LinkedList type의 사용이 가능하다.
val linkedList = LinkedList<Int>()
// 맨 앞에 삽입 [3]
linkedList.addFirst(3)
// index 1에 값 4 삽입 [3, 4]
linkedList.add(1, 4)
// 마지막에 삽입 [3, 4, 5]
linkedList.addLast(5)
// index 0의 값 삭제 [4, 5]
linkedList.removeAt(0)
// 맨 앞의 값 삭제 [5]
linkedList.remove()
// 마지막 값 삭제 []
linkedList.removeLast()
참고 :
[자료구조] 스택 (STACK), 큐(QUEUE) 개념/비교 /활용 예시
[자료구조] 스택 (STACK), 큐(QUEUE) 개념/비교 /활용 예시/ 실생활 활용 스택 (STACK)이란? 📌 스택의 개념 스택(stack)이란 쌓아 올린다는 것을 의미한다. 따라서 스택 자료구조라는 것은 책을 쌓는 것
devuna.tistory.com
https://ko.wikipedia.org/wiki/%EC%8A%A4%ED%83%9D
스택 - 위키백과, 우리 모두의 백과사전
스택(stack)은 제한적으로 접근할 수 있는 나열 구조이다. 그 접근 방법은 언제나 목록의 끝에서만 일어난다. 끝먼저내기 목록(Pushdown list)이라고도 한다. 스택은 한 쪽 끝에서만 자료를 넣거나 뺄
ko.wikipedia.org
https://ko.wikipedia.org/wiki/%ED%81%90_(%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0)
큐 (자료 구조) - 위키백과, 우리 모두의 백과사전
ko.wikipedia.org
https://choheeis.github.io/newblog//articles/2020-10/kotlinQueue
[Kotlin] 8️⃣ 코틀린에서 Queue 사용하기 | choheeis
0️⃣ Queue 란?자료구조 Queue에 관련한 개념은 자료구조에 관련된 이전 포스팅 의 큐 부분에서 알아볼 수 있기 때문에 이 포스팅에서 따로 설명하지 않을 것이다.또한 Queue을 활용하는데 사용되는
choheeis.github.io
https://ko.wikipedia.org/wiki/%EC%97%B0%EA%B2%B0_%EB%A6%AC%EC%8A%A4%ED%8A%B8
연결 리스트 - 위키백과, 우리 모두의 백과사전
ko.wikipedia.org
'Algorithm' 카테고리의 다른 글
| 백준[1182] - 부분수열의 합 (Kotlin) (0) | 2022.01.02 |
|---|---|
| [Kotlin] 정렬 2 (병합정렬, 퀵정렬) (0) | 2021.12.16 |
| [Kotlin] 동적 계획법 (Dynamic Programming, DP) (+ 분할 정복과의 차이) (0) | 2021.12.16 |
| [Kotlin] 정렬 1 (버블정렬, 선택정렬, 삽입정렬) (0) | 2021.12.15 |
| [Kotlin] 자료구조 2 (해쉬 , 트리, 힙) (0) | 2021.12.15 |
![[Kotlin] 자료구조 1 (배열, 스택, 큐, 링크드리스트)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbnDCka%2FbtrnVxA2gMv%2FAAAAAAAAAAAAAAAAAAAAADMR89y9DBAqwrbVAw_54-b5HEbPm8We_BaGwpewweUa%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3DrABV0WGm8QuhAqNBm4bM1xs1674%253D)